Thuật toán là một trong số những khái niệm quan trọng trong thời đại bùng nổ công nghệ hiện nay. Vậy thuật toán là gì? Thuật toán sắp xếp vận hành ra sao? Cùng mangtuyendung.vn tìm hiểu nhé!
Thuật toán khá nổi tiếng là thuật toán tìm kiếm. Bạn có thể nhìn thấy nó ở khá nhiều sản phẩm phần mềm cao cấp hiện tại, điển hình như Google. Bạn có thể nghĩ rằng, công việc tìm kiếm khá là đơn giản, khi bạn lần lượt soi vào từng ô, từng dòng dữ liệu của bạn xem có thứ mà mình tìm kiếm hay không? Sự vận hành của Google yêu cầu 1 thuật toán cực mạnh, và vẫn liên tục cần cải tiến cho đến ngày hôm nay. Vậy thuật toán là gì? Có điều gì thú vị trong các thuật toán sắp xếp? Sự vận hành của thuật toán sắp xếp nổi bọt ra sao?
Mục Lục Bài Viết
I. Giải thích ý nghĩa thuật toán là gì?

Giải thích ý nghĩa thuật toán là gì
1. Thuật toán là gì?
Khái niệm thuật toán hay giải thuật (tiếng anh là Algorithm) trong thuật toán sắp xếp có khá nhiều định nghĩa phức tạp. Có thể lựa chọn định nghĩa dễ hiểu rằng, khái niệm thuật toán trong thuật toán sắp xếp là “thuật” (phương pháp) để giải quyết 1 bài toán.
2. Tại sao cần dùng thuật toán hay thuật toán sắp xếp?
Lập trình chính là quá trình yêu cầu, chỉ thị máy thực hiện, giải quyết 1 công việc, bài toán cụ thể nào đó xuất hiện trong cuộc sống. Mỗi bài toán thực tế sẽ có khá là nhiều cách giải quyết khác nhau. Am hiểu và sử dụng đúng thuật toán là gì, các thuật toán sắp xếp sẽ giúp bạn giải quyết một cách dễ dàng, cùng với độ chính xác được đánh giá cao trong thời gian ngắn nhất.
3. Và không học thuật toán là gì được không?
Thực tế, không học các thuật sắp xếp hay thuật toán thông thường toán vẫn làm được thậm chí làm tốt phần mềm. Kể cả khi bạn làm những sản phẩm có kích thước rất lớn, sử dụng những công nghệ rất mới và hot như AI, BigData hay Blockchain, và cho dù không thành thạo thuật toán nào cả, bạn vẫn có thể xây dựng được hệ thống. Trong trường hợp này, bạn chỉ cần hiểu rõ cách sử dụng và cách ứng dụng cụ thể của công nghệ, chứ không cần nằm hay hiểu rõ thuật toán sắp xếp hay thuật toán là gì bên trong công nghệấy.
4. Rốt cuộc thì thuật toán là gì quan trọng hay không?
Có 1 sự thật rằng, đa phần các sản phẩm phần mềm được sử dụng ngày nay thành công mà không cần hay sử dụng rất ít các thuật toán sắp xếp hay các thuật toán đại trà bên trong nó. Tuy nhiên những sản phẩm có hàm lượng thuật toán cao, và khối lượng trí tuệ lớn, thật sự tạo ra sự khác biệt và thậm chí là thành công lớn hơn những sản phẩm bình thường.
Nhưng tuy thế, thuật toán là gì, các thuật toán sắp xếp ra sao lại không phải yếu tố cốt lõi trực tiếp quyết định thành công và độ ưa chuộng của sản phẩm này. Do đó, việc học thuật toán, sự quan trọng của thuật toán khá là phụ thuộc vào sản phẩm, ứng dụng mà bạn làm.
II. Phân loại thuật toán sắp xếp
1. Sắp xếp ổn định
Một trong các thuật toán sắp xếp được gọi là sắp xếp ổn định nếu sau khi tiến hành sắp xếp thì vị trí tương đối giữa các phần tử được cho trước bằng nhau, không bị thay đổi. Khi thực hiện phân loại một số loại dữ liệu, chỉ một phần dữ liệu của thuật toán sắp xếp là gì được kiểm tra khi xác định thứ tự sắp xếp.
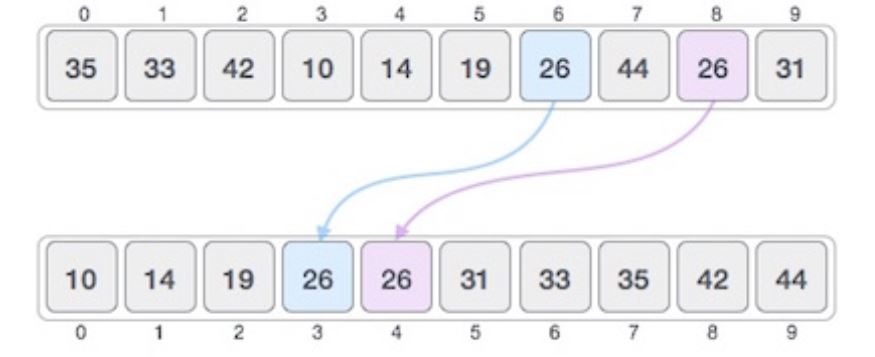 Sắp xếp ổn định
Sắp xếp ổn định
2. Sắp xếp so sánh
Một thuật toán sắp xếp được chuyên môn gọi là sắp xếp so sánh nếu trong quá trình thực hiện thuật toán sắp xếp tương ứng đó ta tiến hành so sánh các khoá và đổi chỗ các phần tử đã cho cho nhau. Đa số các thuật toán sắp xếp là sắp xếp so sánh, riêng hình thức sắp xếp đếm phân phối không phải là thuật toán sắp xếp so sánh.
III. Các khái niệm quan trọng trong giải thuật sắp xếp
1. Thứ tự tăng
Một dãy giá trị dữ liệu được cho trước trong thuật toán sắp xếp được xem như trong thứ tự tăng dần nếu phần tử đứng sau có giá trị lớn hơn phần tử đứng trước. Ví dụ: 1, 3, 5, 6, 9.
2. Thứ tự giảm
Một dãy các dữ liệu giá trị được xem như trong thứ tự giảm dần nếu phần tử trong đó đứng sau nhỏ hơn phần tử đứng trước. Ví dụ: 9, 6, 5, 3, 1.
3. Thứ tự không tăng
Một dãy giá trị trong thuật toán sắp xếp được xem như trong thứ tự không tăng nếu phần tử đứng sau nhỏ hơn hoặc bằng giá trị phần tử đứng trước. Ví dụ: 9, 6, 5, 5, 1. Loại thứ tự này được trực tiếp xuất hiện khi trong một dãy có chứa các giá trị giống nhau (trong ví dụ là 5).
4. Thứ tự không giảm
Một dãy giá trị trong thuật toán sắp xếp được xem như trong thứ tự không giảm nếu phần tử được cho sẵn đứng sau lớn hơn hoặc có thể là bằng phần tử đứng trước. Ví dụ: 1, 5, 5, 6, 9. Loại thứ tự này thường được xuất hiện khi trong một dãy dữ liệu có chứa các giá trị giống nhau (trong ví dụ là 5).
IV. 8 thuật toán sắp xếp phổ biến trong java
8 thuật toán sắp xếp phổ biến trong java
1. Bubble sort (thuật toán sắp xếp nổi bọt – sắp xếp bằng cách đổi chỗ)
Thuật toán sắp xếp nổi bọt là một giải thuật sắp xếp đơn giản. Giải thuật sắp xếp này được tiến hành dựa trên quy trình thực hiện so sánh cặp phần tử liền kề nhau và liên tục tráo đổi thứ tự nếu chúng không theo thứ tự. Đây là điểm đặc biệt của thuật toán sắp xếp nổi bọt.
2. Quick Sort — Sắp xếp nhanh
Giống như Merge sort, thuật toán sắp xếp quick sort là một thuật toán dựa trên quy tắc chia để trị (Divide and Conquer algorithm). Nó thực hiện chọn một phần tử trong mảng làm dữ liệu cho điểm đánh dấu (pivot). Thuật toán sắp xếp đặc biệt này sẽ thực hiện chia mảng thành các mảng con dựa vào pivot đã chọn. Việc lựa chọn pivot là gì ảnh hưởng rất nhiều tới tốc độ sắp xếp. Nhưng máy tính của chúng ta lại không thể biết khi nào thì nên chọn theo cách nào. Dưới đây là một số cách thức khác nhau để chọn pivot thường được sử dụng:
- Luôn chọn phần tử được sắp xếp đầu tiên của mảng.
- Luôn chọn phần tử được sắp xếp cuối cùng của mảng.
- Chọn một phần tử theo cách random.
- Chọn một phần tử có dữ liệu giá trị nằm giữa mảng (median element).
3. Simple selection sort.
Thuật toán sắp xếp selection sort thực hiện sắp xếp một mảng bằng cách đi tìm phần tử tương ứng có giá trị nhỏ nhất (giả sử với sắp xếp mảng tăng dần) trong đoạn đã cho chưa được sắp xếp. Sau đó thực hiện đổi chỗ phần tử nhỏ nhất đó với phần tử ở vị trí đầu đoạn chưa được sắp xếp sẵn (không phải đầu mảng). Thuật toán sắp xếp này sẽ chia mảng làm 2 mảng con
- Một mảng con đã được thực hiện sắp xếp
- Một mảng con chưa được thực hiện sắp xếp
Tại mỗi bước lặp của thuật toán sắp xếp này, phần tử nhỏ nhất ở mảng con chưa được sắp xếp sẽ được thực hiện di chuyển về đoạn đã sắp xếp.
4. Heap Sort
Giải thuật Heapsort hay còn được người dùng gọi là giải thuật vun đống, có thể được xem như phiên bản cải tiến của thuật toán sắp xếp Selection Sort khi chia các phần tử thành 2 mảng con.
- 1 mảng các phần tử đã được thực hiện sắp xếp.
- 1 mảng các phần tử chưa được thực hiện sắp xếp.
5. Simple insertion sort.
Sắp xếp chèn (insertion sort) là một thuật toán sắp xếp có khả năng bắt chước cách sắp xếp quân bài của những người chơi bài. Muốn sắp một bộ bài theo trật tự thì người chơi bài sẽ thực hiện rút lần lượt từ quân thứ 2, so với các quân đứng trước nó để có thể chèn vào vị trí thích hợp.
6. Shell sort.
Shell Sort là một giải thuật sắp xếp quan trọng mang lại hiệu quả cao dựa trên giải thuật sắp xếp chèn (Insertion Sort). Giải thuật này đặc biệt ở chỗ nó tránh các trường hợp phải thực hiện tráo đổi vị trí của hai phần tử xa nhau trong giải thuật sắp xếp chọn (nếu như phần tử trong thuật toán sắp xếp nhỏ hơn ở vị trí bên phải khá xa so với phần tử lớn hơn bên trái).
7. Merge sort.
Giống như Quick sort, Merge sort là một thuật toán sắp xếp chia để trị. Thuật toán này thực hiện chia mảng cần sắp xếp thành 2 nửa. Tiếp tục lặp lại việc này ở các nửa mảng thuật toán đã chia. Sau cùng gộp các nửa đó thành mảng tương ứng đã sắp xếp. Hàm merge() được sử dụng để có thể gộp hai nửa mảng. Hàm merge(arr, l, m, r) là phần tiến trình quan trọng nhất của thuật toán sẽ gộp hai nửa mảng thành 1 mảng sắp xếp, các nửa mảng tiếp theo là arr[l…m] và arr[m+1…r] sau khi gộp sẽ tạo thành một mảng duy nhất đã sắp xếp.
8. Radix sort.
Radix Sort là thuật toán sắp xếp đặc biệt, nó tiếp cận theo một hướng hoàn toàn khác các thuật toán sắp xếp khác được nói bên trên. Thay vì cơ sở để sắp xếp luôn là việc so sánh giá trị của 2 phần tử thì thuật toán sắp xếp Radix Sort lại dựa theo nguyên tắc phân loại thư tương tự với bưu điện (Postman’s sort).
Radix sort không quan tâm đến quá trình so sánh giá trị của 2 phần tử mà bản thân việc phân loại và kết hợp với thứ tự phân loại sẽ tạo ra thứ tự cho các phần tử.
V. Kết luận
Thuật toán và sử dụng thuật toán sắp xếp là lợi thế lớn trong việc lập trình, vận hành máy móc, thiết bị và các phần mềm công nghệ khác. mangtuyendung hi vọng qua bài viết này bạn đã có cái nhìn bao quát về những thuật toán sắp xếp quan trọng, ví dụ như thuật toán sắp xếp nổi bọt, có thể ứng dụng nhiều trong công việc thực tế.